第十九章 Bodies in Straight Line

1. 定义

　　当天体位于同一个天球大圆时，我们称之为天体处在同一”直线”上。
　　假设有三个天体,赤道系坐标分别为$(α_1,δ_1),(α_2,δ_2),(α_3,δ_3)$，当它们”共线”时，有：$$\tan δ_1\sin (α_2-α_3)+\tan δ_2\sin (α_3-α_1)+\tan δ_3\sin (α_1-α_2)=0$$ 　　上述公式对黄道坐标系同样适用。

　　利用该公式，我们就可以插值求得共线的时间点

2. 计算行星与两个恒星共线的时间点

　　对于恒星，我们可以认为在一定观测时间范围内是静止的。所以在进行插值计算时，应该当做常数。如$(α_1,δ_1),(α_2,δ_2)$为恒星坐标，则插值时保持不变。
　　对于运动的行星，考虑一段时间范围内的坐标，进行插值并求零点。

// Time computes the time at which a moving body is on a straight line (great
// circle) between two fixed points, such as stars.
//
// Coordinates may be right ascensions and declinations or longitudes and
// latitudes.  Fixed points are r1, d1, r2, d2.  Moving body is an ephemeris
// of 5 rows, r3, d3, starting at time t1 and ending at time t5.  Time scale
// is arbitrary.
//
// Result is time of alignment.
// 计算一个运动的天体和另外两个在观测时间内默认为不动的天体在一条直线上的时间点
func Time(r1, d1, r2, d2 unit.Angle, r3, d3 []unit.Angle, t1, t5 float64) (float64, error) {
	if len(r3) != 5 || len(d3) != 5 {
		return 0, errors.New("r3, d3 must be length 5")
	}
	gc := make([]float64, 5)
	for i, r3i := range r3 {
		// (19.1) p. 121
		gc[i] = d1.Tan()*(r2-r3i).Sin() +
			d2.Tan()*(r3i-r1).Sin() +
			d3[i].Tan()*(r1-r2).Sin()
	}
	l5, err := interp.NewLen5(t1, t5, gc)
	if err != nil {
		return 0, err
	}
	return l5.Zero(false)
}

3. 计算3点”近似共线”时的球面角和离共线大圆的角距离

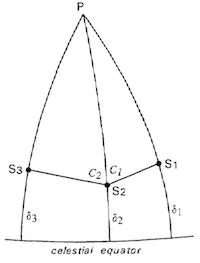　　如上图，$S_1,S_2,S_3$为三个天体，此时它们几乎”共线”,$C_1$为球面角$\angle PS_2S_1$，$C_2$为球面角$\angle PS_2S_3$，我们所求的就是球面角$\angle S_1S_2S_3$以及$S_2$与经过$S_1,S_3$的大圆之间的角距离（可以看作离共线还差多少度）

• Meeus 计算三天体球面角$\angle S_1S_2S_3$

\begin{cases} \tan C_1 &= \frac {\sin (α_2-α_1)}{\cos δ_2\tan δ_1-\sin δ_2\cos (α_2-α_1)}\\[2ex] \tan C_2 &= \frac {\sin (α_3-α_2)}{\cos δ_2\tan δ_3-\sin δ_2\cos (α_3-α_2)} \end{cases} 　　$C_1 + C_2$即为所求

// Angle returns the angle between great circles defined by three points.
//
// Coordinates may be right ascensions and declinations or longitudes and
// latitudes.  If r1, d1, r2, d2 defines one line and r2, d2, r3, d3 defines
// another, the result is the angle between the two lines.
//
// Algorithm by Meeus.
// 计算第一点第二点经过的大圆和第二点第三点经过的大圆之间的角度
func Angle(r1, d1, r2, d2, r3, d3 unit.Angle) unit.Angle {
	sd2, cd2 := d2.Sincos()
	sr21, cr21 := (r2 - r1).Sincos()
	sr32, cr32 := (r3 - r2).Sincos()
	C1 := math.Atan2(sr21, cd2*d1.Tan()-sd2*cr21)
	C2 := math.Atan2(sr32, cd2*d3.Tan()-sd2*cr32)
	return unit.Angle(C1 + C2)
}

• Meeus 计算$S_2$与经过$S_1,S_3$的大圆之间的角距离

　　先计算： \begin{cases} X_1 &= \cos δ_1\cos α_1\\[2ex] Y_1 &= \cos δ_1\sin α_1\\[2ex] Z_1 &= \sin δ_1 \end{cases} \begin{cases} X_2 &= \cos δ_2\cos α_2\\[2ex] Y_2 &= \cos δ_2\sin α_2\\[2ex] Z_2 &= \sin δ_2 \end{cases} \begin{cases} A &= Y_1Z_2-Z_1Y_2\\[2ex] B &= Z_1X_2-X_1Z_2\\[2ex] C &= X_1Y_2-Y_1X_2 \end{cases} $$m = \tan α_0, n = \frac {\tan δ_0}{\cos α_0}$$ 　　则，$$\sin ω = \frac {A+Bm+Cn}{\sqrt {A^2+B^2+C^2}\sqrt{1+m^2+n^2}}$$ 　　ω即为所求

// Error returns an error angle of three nearly co-linear points.
//
// For the line defined by r1, d1, r2, d2, the result is the anglular distance
// between that line and r0, d0.
//
// Algorithm by Meeus.
// 计算一点到由另外两点组成的大圆之间的角距离
func Error(r1, d1, r2, d2, r0, d0 unit.Angle) unit.Angle {
	sr1, cr1 := r1.Sincos()
	sd1, cd1 := d1.Sincos()
	sr2, cr2 := r2.Sincos()
	sd2, cd2 := d2.Sincos()
	X1 := cd1 * cr1
	X2 := cd2 * cr2
	Y1 := cd1 * sr1
	Y2 := cd2 * sr2
	Z1 := sd1
	Z2 := sd2
	A := Y1*Z2 - Z1*Y2
	B := Z1*X2 - X1*Z2
	C := X1*Y2 - Y1*X2
	m := r0.Tan()
	n := d0.Tan() / r0.Cos()
	return unit.Angle(math.Asin((A + B*m + C*n) /
		(math.Sqrt(A*A+B*B+C*C) * math.Sqrt(1+m*m+n*n))))
}

• Pessens 同时计算上述两个量

\begin{cases} a_1 &= \cos δ_1\cos α_1\\[2ex] a_2 &= \cos δ_2\cos α_2\\[2ex] a_3 &= \cos δ_3\cos α_3\\[2ex] \end{cases} \begin{cases} b_1 &= \cos δ_1\sin α_1\\[2ex] b_2 &= \cos δ_2\sin α_2\\[2ex] b_3 &= \cos δ_3\sin α_3\\[2ex] \end{cases} \begin{cases} c_1 &= \sin δ_1\\[2ex] c_2 &= \sin δ_2\\[2ex] c_3 &= \sin δ_3\\[2ex] \end{cases} \begin{cases} l_1 &= b_1c_2-b_2c_1\\[2ex] l_2 &= b_2c_3-b_3c_2\\[2ex] l_3 &= b_1c_3-b_3c_1\\[2ex] \end{cases} \begin{cases} m_1 &= c_1a_2-c_2a_1\\[2ex] m_2 &= c_2a_3-c_3a_2\\[2ex] m_3 &= c_1a_3-c_3a_1\\[2ex] \end{cases} \begin{cases} n_1 &= a_1b_2-a_2b_1\\[2ex] n_2 &= a_2b_3-a_3b_2\\[2ex] n_3 &= a_1b_3-a_3b_1\\[2ex] \end{cases} 　　则有： \begin{cases} \cos ψ &= \frac {l_1l_2+m_1m_2+n_1n_2}{\sqrt {l_1^2+m_1^2+n_1^2}\sqrt{l_2^2+m_2^2+n_2^2}}\\[2ex] \sin ω &= \frac {a_2l_3+b_2m_3+c_2n_3}{\sqrt {a_2^2+b_2^2+c_2^2}\sqrt {l_3^2+m_3^2+n_3^2}} \end{cases} 　　ψ，ω即为所求。ψ可能与 Meeus 方法求解的值互余180°。（平面的夹角有两个，互余180°）

// AngleError returns both an angle as in the function Angle, and an error
// as in the function Error.
//
// The algorithm is by B. Pessens.
// Angle和 Error 的合体版
// Angle 的值可能和之前 Angle 中计算的值互余180°（想象一下两个面的夹角）
func AngleError(r1, d1, r2, d2, r3, d3 unit.Angle) (ψ, ω unit.Angle) {
	sr1, cr1 := r1.Sincos()
	sd1, cd1 := d1.Sincos()
	sr2, cr2 := r2.Sincos()
	sd2, cd2 := d2.Sincos()
	sr3, cr3 := r3.Sincos()
	sd3, cd3 := d3.Sincos()
	a1 := cd1 * cr1
	a2 := cd2 * cr2
	a3 := cd3 * cr3
	b1 := cd1 * sr1
	b2 := cd2 * sr2
	b3 := cd3 * sr3
	c1 := sd1
	c2 := sd2
	c3 := sd3
	l1 := b1*c2 - b2*c1
	l2 := b2*c3 - b3*c2
	l3 := b1*c3 - b3*c1
	m1 := c1*a2 - c2*a1
	m2 := c2*a3 - c3*a2
	m3 := c1*a3 - c3*a1
	n1 := a1*b2 - a2*b1
	n2 := a2*b3 - a3*b2
	n3 := a1*b3 - a3*b1
	ψ = unit.Angle(math.Acos((l1*l2 + m1*m2 + n1*n2) /
		(math.Sqrt(l1*l1+m1*m1+n1*n1) * math.Sqrt(l2*l2+m2*m2+n2*n2))))
	ω = unit.Angle(math.Asin((a2*l3 + b2*m3 + c2*n3) /
		(math.Sqrt(a2*a2+b2*b2+c2*c2) * math.Sqrt(l3*l3+m3*m3+n3*n3))))
	return
}