第二十七章 分点和至点 Equinoxes and Solstices
分点(英语:equinox,或称二分点)是想像中天球赤道在天球上的位置,是每年太阳穿过天球赤道和黄道在天球上交点的天文事件[1],这造成地球上各地的白天和夜晚几乎等长。
二至点(亦称至点)可以是太阳在一年之中离地球赤道最远的两个事件中的任何一个,英文的字源(solstice) 来自拉丁文的太阳(sol)和保持直立(sistere),因为在至点时太阳直射的地球纬度是他能抵达的最南或最北的极值,而至点所在之日是一年之中日夜长短差异最大的一天。
分点和至点时刻是指:太阳的地心视黄经(含光行差和章动)为90的整数倍时对应的时刻。因太阳黄纬不是真正为零的,所以在分点时刻太阳赤纬也不是真正为零的。

1. 近似时刻计算(最大误差1分钟)
先找到平分点或平至点$JDE_0$
当$year \in [-1000,1000)$时,
\begin{cases}
Y = \frac {year}{1000}\\[2ex]
春分点:JDE_0 = 1721139.29189 + 365242.13740Y + 0.06134Y^2 + 0.00111Y^3 - 0.00071Y^4\\[2ex]
夏至点:JDE_0 = 1721233.25401 + 365241.72562Y - 0.05323Y^2 + 0.00907Y^3 + 0.00025Y^4\\[2ex]
秋分点:JDE_0 = 1721325.70455 + 365242.49558Y - 0.11677Y^2 - 0.00297Y^3 + 0.00074Y^4\\[2ex]
冬至点:JDE_0 = 1721414.39987 + 365242.88257Y - 0.00769Y^2 - 0.00933Y^3 - 0.00006Y^4\\[2ex]
\end{cases}
当$year \in [1000,3000]$时,
\begin{cases}
Y = \frac {year-2000}{1000}\\[2ex]
春分点:JDE_0 = 2451623.80984 + 365242.37404Y + 0.05169Y^2 - 0.00411Y^3 - 0.00057Y^4\\[2ex]
夏至点:JDE_0 = 2451716.56767 + 365241.62603Y + 0.00325Y^2 + 0.00888Y^3 - 0.00030Y^4\\[2ex]
秋分点:JDE_0 = 2451810.21715 + 365242.01767Y - 0.11575Y^2 + 0.00337Y^3 + 0.00078Y^4\\[2ex]
冬至点:JDE_0 = 2451900.05952 + 365242.74049Y - 0.06223Y^2 - 0.00823Y^3 + 0.00032Y^4\\[2ex]
\end{cases}
再计算
\begin{cases}
T &= \frac {JDE_0 - 2451545.0}{36525}\\[2ex]
W &= 35999°.373T - 2°.47\\[2ex]
Δλ &= 1 + 0.0334\cos W + 0.0007\cos (2W)\\[2ex]
S &= \sum A\cos(B+CT)
\end{cases}
其中$A,B,C$分别为下表中的系数项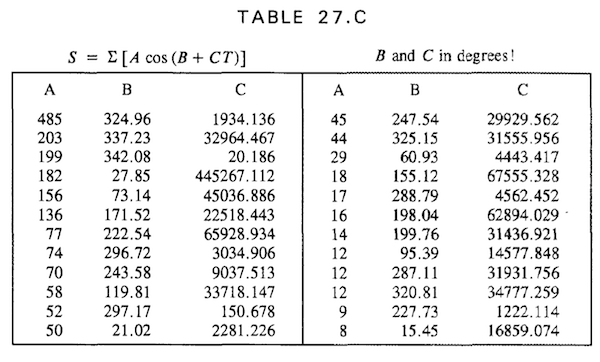 那么$$JDE = JDE_0 + \frac {0.00001S}{Δλ} days$$
注意此时得到的力学时DT,可以按需再转为UT
那么$$JDE = JDE_0 + \frac {0.00001S}{Δλ} days$$
注意此时得到的力学时DT,可以按需再转为UT
var (
mc0 = []float64{1721139.29189, 365242.13740, .06134, .00111, -.00071}
jc0 = []float64{1721233.25401, 365241.72562, -.05232, .00907, .00025}
sc0 = []float64{1721325.70455, 365242.49558, -.11677, -.00297, .00074}
dc0 = []float64{1721414.39987, 365242.88257, -.00769, -.00933, -.00006}
mc2 = []float64{2451623.80984, 365242.37404, .05169, -.00411, -.00057}
jc2 = []float64{2451716.56767, 365241.62603, .00325, .00888, -.00030}
sc2 = []float64{2451810.21715, 365242.01767, -.11575, .00337, .00078}
dc2 = []float64{2451900.05952, 365242.74049, -.06223, -.00823, .00032}
)
type term struct {
a, b, c float64
}
var terms = []term{
{485, 324.96, 1934.136},
{203, 337.23, 32964.467},
{199, 342.08, 20.186},
{182, 27.85, 445267.112},
{156, 73.14, 45036.886},
{136, 171.52, 22518.443},
{77, 222.54, 65928.934},
{74, 296.72, 3034.906},
{70, 243.58, 9037.513},
{58, 119.81, 33718.147},
{52, 297.17, 150.678},
{50, 21.02, 2281.226},
{45, 247.54, 29929.562},
{44, 325.15, 31555.956},
{29, 60.93, 4443.417},
{18, 155.12, 67555.328},
{17, 288.79, 4562.452},
{16, 198.04, 62894.029},
{14, 199.76, 31436.921},
{12, 95.39, 14577.848},
{12, 287.11, 31931.756},
{12, 320.81, 34777.259},
{9, 227.73, 1222.114},
{8, 15.45, 16859.074},
}
// March returns the JDE of the March equinox for the given year.
// 计算y年春分点力学时,y∈[-1000,3000]
//
// Results are valid for the years -1000 to +3000.
//
// Accuracy is within one minute of time for the years 1951-2050.
func March(y int) float64 {
if y < 1000 {
return eq(y, mc0)
}
return eq(y-2000, mc2)
}
// June returns the JDE of the June solstice for the given year.
// 计算y年夏至点力学时,y∈[-1000,3000]
//
// Results are valid for the years -1000 to +3000.
//
// Accuracy is within one minute of time for the years 1951-2050.
func June(y int) float64 {
if y < 1000 {
return eq(y, jc0)
}
return eq(y-2000, jc2)
}
// September returns the JDE of the September equinox for the given year.
// 计算y年秋分点力学时,y∈[-1000,3000]
//
// Results are valid for the years -1000 to +3000.
//
// Accuracy is within one minute of time for the years 1951-2050.
func September(y int) float64 {
if y < 1000 {
return eq(y, sc0)
}
return eq(y-2000, sc2)
}
// December returns the JDE of the December solstice for a given year.
// 计算y年冬至点力学时,y∈[-1000,3000]
//
// Results are valid for the years -1000 to +3000.
//
// Accuracy is within one minute of time for the years 1951-2050.
func December(y int) float64 {
if y < 1000 {
return eq(y, dc0)
}
return eq(y-2000, dc2)
}
func eq(y int, c []float64) float64 {
J0 := base.Horner(float64(y)*.001, c...)
T := base.J2000Century(J0)
W := 35999.373*math.Pi/180*T - 2.47*math.Pi/180
Δλ := 1 + .0334*math.Cos(W) + .0007*math.Cos(2*W)
S := 0.
for i := len(terms) - 1; i >= 0; i-- {
t := &terms[i]
S += t.a * math.Cos((t.b+t.c*T)*math.Pi/180)
}
return J0 + .00001*S/Δλ
}
2. 高精度分至点时刻计算
先用低精度方法算出近似时刻,再采用VSOP87理论计算出该时刻的太阳视黄经$λ$,
再根据各个分至点的几何度数按以下公式求该近似时刻的修正量,循环迭代,直至满足要求。
$$+58\sin (k90° - λ)$$
其中k=0,1,2,3分别对应春夏秋冬四个分至点
// March2 returns a more accurate JDE of the March equinox.
// 高精度计算春分点力学时
//
// Result is accurate to one second of time.
//
// Parameter e must be a V87Planet object representing Earth, obtained with
// the package planetposition and code similar to
//
// e, err := planetposition.LoadPlanet(planetposition.Earth, "")
// if err != nil {
// ....
//
// See example under June2.
func March2(y int, e *pp.V87Planet) float64 {
if y < 1000 {
return eq2(y, e, 0, mc0)
}
return eq2(y-2000, e, 0, mc2)
}
// June2 returns a more accurate JDE of the June solstice.
// 高精度计算夏至点力学时
//
// Result is accurate to one second of time.
//
// Parameter e must be a V87Planet object representing Earth, obtained with
// the package planetposition.
func June2(y int, e *pp.V87Planet) float64 {
if y < 1000 {
return eq2(y, e, math.Pi/2, jc0)
}
return eq2(y-2000, e, math.Pi/2, jc2)
}
// September2 returns a more accurate JDE of the September equinox.
// 高精度计算秋分点力学时
//
// Result is accurate to one second of time.
//
// Parameter e must be a V87Planet object representing Earth, obtained with
// the package planetposition and code similar to
//
// e, err := planetposition.LoadPlanet(planetposition.Earth, "")
// if err != nil {
// ....
//
// See example under June2.
func September2(y int, e *pp.V87Planet) float64 {
if y < 1000 {
return eq2(y, e, math.Pi, sc0)
}
return eq2(y-2000, e, math.Pi, sc2)
}
// December2 returns a more accurate JDE of the December solstice.
// 高精度计算冬至点力学时
//
// Result is accurate to one second of time.
//
// Parameter e must be a V87Planet object representing Earth, obtained with
// the package planetposition and code similar to
//
// e, err := planetposition.LoadPlanet(planetposition.Earth, "")
// if err != nil {
// ....
//
// See example under June2.
func December2(y int, e *pp.V87Planet) float64 {
if y < 1000 {
return eq2(y, e, math.Pi*3/2, dc0)
}
return eq2(y-2000, e, math.Pi*3/2, dc2)
}
//先用低精度方法算出近似时刻,再采用VSOP87理论计算出该时刻的太阳视黄经λ,
//再根据各个分至点的几何度数求该近似时刻的修正量,循环迭代,直至满足要求。
func eq2(y int, e *pp.V87Planet, q unit.Angle, c []float64) float64 {
J0 := base.Horner(float64(y)*.001, c...)
for {
λ, _, _ := solar.ApparentVSOP87(e, J0)
c := 58 * (q - λ).Sin() // (27.1) p. 180
J0 += c
if math.Abs(c) < .000005 {
break
}
}
return J0
}
