第十四章 The Parallactic Angle

1. 什么是Parallactic Angle

　　Parallactic is NOT Parallax
　　这里所说的 Parallactic Angle 并不是 Parallax，Parallax是从两个不同的视点看同一物体时这两条视线之间的夹角(或半角)，主要用来测定物体的距离，如秒差距这一距离单位就是利用视差角来定义的。
　　In spherical astronomy, the parallactic angle is the angle between the great circle through a celestial object and the zenith(天体与天顶所在的大圆，即天球地平经线), and the hour circle of the object（天体的时角，即天球赤道经线）.It is usually denoted q. In the triangle zenith—object—celestial pole, the parallactic angle will be the position angle of the zenith at the celestial object. Despite its name, this angle is unrelated with parallax. The parallactic angle is zero when the object crosses the meridian.
　　换句话说，就是天体地平经线与天体赤道经线之间的角度。

2. 计算Parallactic Angle

$$\tan q=\frac {\sin H}{\tan φ\cos δ -\sin δ\cos H}$$ 　　式中，$φ$是观测站地理纬度,$δ$是天体的赤纬，$H$是该时刻的时角。

如何推导？

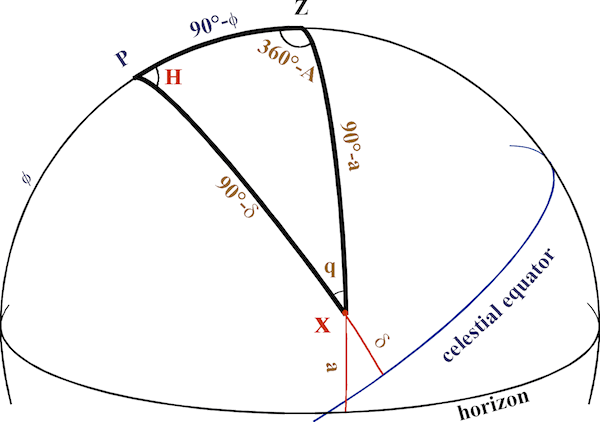
如上图，P为天球极点，Z为天顶，X为观测目标，此时观测点为球心（地平坐标系），
由观测站地理纬度$φ$可知，弧长 $\newcommand{arc}[1]{\stackrel{\Large\frown}{#1}}\arc{PZ}= 90°-φ$,
由天体的赤纬$δ$可知，弧长 $\newcommand{arc}[1]{\stackrel{\Large\frown}{#1}}\arc{PX}= 90°-δ$,
由天体的时角$H$可知，球面角 $\angle ZPX = H$,
假设 X 的仰角为$a$,则弧长 $\newcommand{arc}[1]{\stackrel{\Large\frown}{#1}}\arc{ZX}= 90°-a$,
根据球面余弦公式，我们有 \begin{cases} \cos (90°-a) &= \cos (90°-φ)\cos (90°-δ) + \sin (90°-φ)\sin (90°-δ)\cos H\\[2ex] \cos (90°-φ) &= \cos (90°-a)\cos (90°-δ) + \sin (90°-a)\sin (90°-δ)\cos q \end{cases} 即 \begin{cases} \sin a &= \sin φ\sin δ + \cos φ\cos δ\cos H, &(1)\\[2ex] \sin φ &= \sin a\sin δ + \cos a\cos δ\cos q, &(2) \end{cases} 根据正弦公式，我们有$$\frac {\sin H}{\cos a} = \frac {\sin q}{\cos φ},\ \ \ (3)$$ 由(2)(3)可得 \begin{align} \tan q &= \frac {\sin q}{\cos q}\\[2ex] & = \frac {\frac {\sin H\cos φ}{\cos a}}{\frac {\sin φ-\sin a\sin δ}{\cos a\cos δ}}\\[2ex] & = \frac {\sin H\cos φ\cos δ}{\sin φ-\sin a\sin δ} \end{align} 再将(1)代入上式中， \begin{align} \tan q & = \frac {\sin H\cos φ\cos δ}{\sin φ-\sin δ(\sin φ\sin δ + \cos φ\cos δ\cos H)}\\[2ex] & = \frac {\sin H\cos φ\cos δ}{\sin φ\cos^2δ - \cos φ\cos δ\sin δ\cos H}\\[2ex] & = \frac {\sin H}{\tan φ\cos δ - \sin δ\cos H} \end{align} 得证

另一种直接证明

　　当天体位于中天时恰好与天顶重合，则有$δ=φ$，此时$\tan q = \frac 00$，没有意义，也就是说角度由-90°跳到90°。
　　当天体位于地平线上时，即$a=0°$时，由(2)式直接可得$$\cos q = \frac {\sin φ}{\cos δ}$$ 与时角$H$无关

// ParallacticAngle returns parallactic angle of a celestial object.
//
//	φ is geographic latitude of observer.观测点地理纬度
//	δ is declination of observed object.天体赤纬
//	H is hour angle of observed object.天体赤经（时角）
//  计算天体的Parallactic Angle
func ParallacticAngle(φ, δ unit.Angle, H unit.HourAngle) unit.Angle {
	sδ, cδ := δ.Sincos()
	sH, cH := H.Sincos()
	// (14.1) p. 98
	return unit.Angle(math.Atan2(sH, φ.Tan()*cδ-sδ*cH))
}

// ParallacticAngleOnHorizon is a special case of ParallacticAngle.
//
// The hour angle is not needed as an input and the math inside simplifies.
// 当天体位于地平线上时，计算Parallactic Angle，与时角无关
func ParallacticAngleOnHorizon(φ, δ unit.Angle) unit.Angle {
	return unit.Angle(math.Acos(φ.Sin() / δ.Cos()))
}