第十三章 坐标的转换 Transformation of Coordinates
1. 天球坐标系统
天球坐标系统,是天文学上用来描绘天体在天球上位置的坐标系统。有许多不同的坐标系统都使用球面坐标投影在天球上,类似于使用在地球表面的地理坐标系统。这些坐标系统的不同处只在用来将天空分割成两个相等半球的大圆,也就是基面的不同。例如,地理坐标系统的基面是地球的赤道。每个坐标系统的命名都是依据其所选择的基面。
\begin{array}{c|ccc}
坐标系统 & 基面 & 极 & 坐标 \\
\hline
地平 & 地平面 & 天顶/天底 & 高度(也称为仰角) - 方位 - 子午圈 \\
赤道 & 天球赤道 & 天极 & 赤纬 - 赤经或时角 \\
黄道 & 黄道 & 黄极 & 黄纬 - 黄经 \\
银河 & 银河平面 & 银极 & 银经 - 银纬 \\
超星系 & 超星系平面 & & \\
\end{array}
2. 地平坐标系
地平坐标系,又作地平座标系,是天球坐标系统中的一种,以观测者所在地为中心点,所在地的地平线作为基础平面,将天球适当的分成能看见的上半球和看不见(被地球本身遮蔽)的下半球。上半球的顶点(最高点)称为天顶,下半球的顶点(最低点)称为地底。
地平坐标系统是:
- 高度角(Altitude, Alt)或仰角又称地平纬度,是天体和观测者所在地的地平线的夹角,有时就称为高度或海拔标高(elevation, geometric height)。
- 方位角(Azimuth, Az)又称地平经度,是沿着地平线测量的角度(由正北方为起点向东方测量)。
因此地平坐标系有时也被称为高度/方位(Alt/Az)坐标系统。
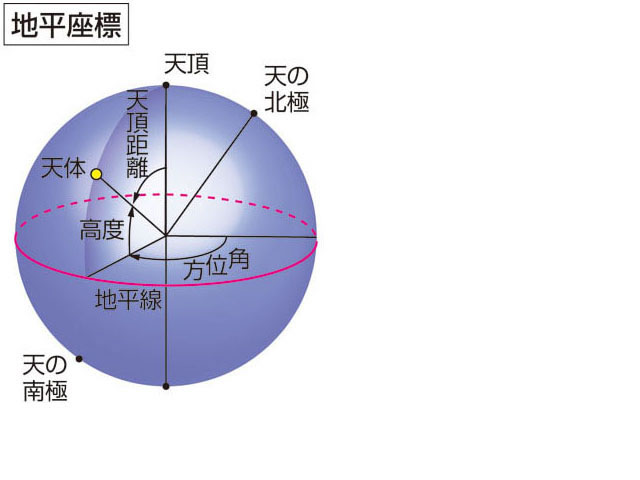
注:方位角的测量可以从北点向东测量,也可从南点向西测量,两者相差180°。天文学家习惯从南点开始测量。
3. 赤道坐标系
赤道坐标系统,又作赤道座标系统,大概是使用得最广泛的天球坐标系统,他的元素是:
- 赤纬Declination( $\delta$ )
- 赤经Right ascension( $\alpha$ )-也记为RA
他与地理坐标系统非常相似,因为两者使用相同的基准平面和相同的极点。地球的赤道在天球上的投影就称为天球赤道,相同的,地理极点在天球上的投影就是天极。
他有两种变化:
- 时角系统像地理坐标系统一样,被固定在地球的表面上。
- 赤经系统被固定于恒星上(实际上并非如此,请参考岁差和章动)。
因此,在经过一夜或数个夜晚,就能看出来星星在天空中的位置移动了,当然,这并非恒星在天球上的运动,只是地球运动造成的。因为岁差和章动的影响,在相当长的时间间隔下所做的观测,就必须注明所使用的特殊历元,为行星、恒星、星系等等的位置做记录。现在使用的历元是J2000.0分点,稍早期使用的是B1950.0分点。
赤道坐标系统中与纬度相似的值是赤纬(缩写为Dec.),是天体在天球赤道上方或下方的角度。与经度对应的是赤经(缩写为RA),是与春分点的角度距离,不同于经度的是赤经以时、分、秒为单位,而非度、分、秒。因为地球的运动造成赤道坐标系统的视运动,就会造成恒星时和时角的相对变化。将天球运转一周的时间定为24小时,所以每小时天球会转动15度(360º / 24h = 15)。
赤道坐标系统也是赤道仪上很普通的设备,也就是定位圈。定位圈与星图或星历表上的位置结合,可以让赤道仪很容易的指向已知天体在天球上的位置。
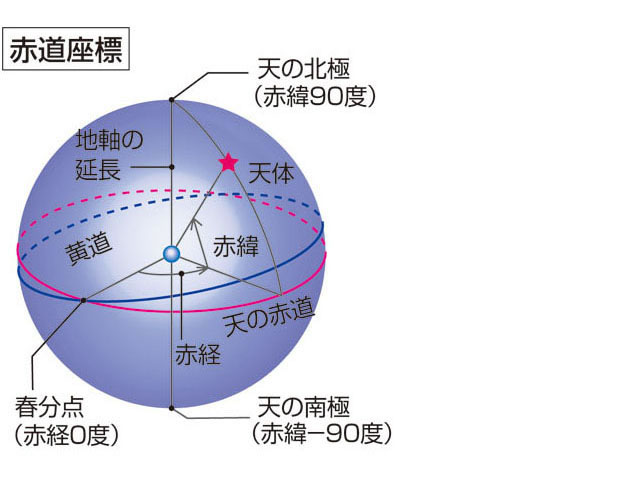
4. 黄道坐标系
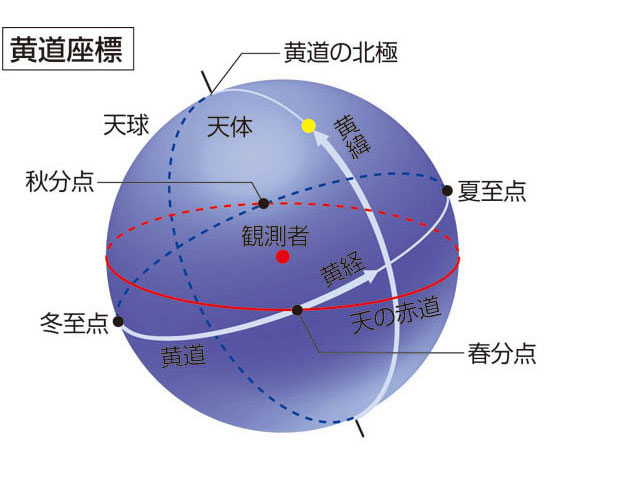
黄道是由地球上观察太阳一年中在天球上的视运动所通过的路径,若以地球“不动”作参照的话就是太阳绕地球公转的轨道平面(黄道面)在天球上的投影。
黄道与天赤道相交于两点:春分点与秋分点(这两点称二分点);而黄道对应的两个几何极是北黄极(在天龙座)、与南黄极 (在剑鱼座)。
在黄道上与黄道平行的小圆称黄纬,符号β,以由黄道面向北黄极方向为正值(0°至90°),向南黄极方向则为负值。垂直黄道的经度称黄经,符号为λ,由春分点起由西向东量度(0°至360°)。像赤道坐标系中的赤经一样,以春分点做为黄经的起点。
因为地轴有进动现象,此坐标系的两个黄极亦会因岁差影响而使坐标数值逐渐移动,计算时必须说明坐标系参照的历元。现常采用的是J2000.0历元(之前的出版物多以B1950.0历元),在天文年历这类精度较高的刊物中,则参考当天或当月之瞬时分点计算。
此坐标系特别适合标示太阳系内天体的位置,大多数行星(水星和冥王星除外)与许多小行星轨道平面与黄道的倾角都很小,故其黄纬值(β)都不大。
5. 坐标系转换
- $λ$和$β$代表黄经和黄纬
- $α$和$δ$代表赤经和赤纬
- $φ,A,h$代表观察者纬度,方位角,和仰角,其中默认A从南点向西测量
- $ε$黄赤交角
注:如果给定的为视坐标,在转换为本地地平坐标时要先将视赤经(时角)转换为本地时角。
例如:如果θ是本地恒星时,$θ_0$ 是格林尼治恒星时,L 是观者站经度(从格林尼治向西为正,东为负),那么本地时角为$ θ - α 或 θ_0 - L – α$
5.1 赤道转黄道($α,δ\ \Rightarrow\ λ,β$)
\begin{align} \sin β &=\cos ε\sin δ-\sin α\cos δ\sin ε\\[2ex] \cos λ\cos β &=\cos α\cos δ\\[2ex] \sin λ\cos β &=\sin ε\sin δ+\sin α\cos δ\cos ε \end{align}
// Obliquity represents the obliquity of the ecliptic.
// 黄赤交角对应的 sin,cos 值
type Obliquity struct {
S, C float64 // sine and cosine of obliquity
}
// NewObliquity constructs a new Obliquity.
//
// Struct members are initialized from the given value ε of the obliquity of
// the ecliptic.
// 计算黄赤交角对应的 sin,cos 值
func NewObliquity(ε unit.Angle) *Obliquity {
r := &Obliquity{}
r.S, r.C = ε.Sincos()
return r
}
// Ecliptic coordinates are referenced to the plane of the ecliptic.
// 黄道坐标结构
type Ecliptic struct {
Lon unit.Angle // Longitude (λ)黄经
Lat unit.Angle // Latitude (β)黄纬
}
// EqToEcl converts equatorial coordinates to ecliptic coordinates.
// 赤道转黄道
func (ecl *Ecliptic) EqToEcl(eq *Equatorial, ε *Obliquity) *Ecliptic {
ecl.Lon, ecl.Lat = EqToEcl(eq.RA, eq.Dec, ε.S, ε.C)
return ecl
}
// EqToEcl converts equatorial coordinates to ecliptic coordinates.
//
// α: right ascension coordinate to transform
// δ: declination coordinate to transform
// sε: sine of obliquity of the ecliptic
// cε: cosine of obliquity of the ecliptic
//
// Results:
//
// λ: ecliptic longitude黄经
// β: ecliptic latitude黄纬
// 赤道转黄道
func EqToEcl(α unit.RA, δ unit.Angle, sε, cε float64) (λ, β unit.Angle) {
sα, cα := α.Sincos()
sδ, cδ := δ.Sincos()
λ = unit.Angle(math.Atan2(sα*cε+(sδ/cδ)*sε, cα)) // (13.1) p. 93
β = unit.Angle(math.Asin(sδ*cε - cδ*sε*sα)) // (13.2) p. 93
return
}
5.2 黄道转赤道($λ,β\ \Rightarrow\ α,δ$)
\begin{align} \sin δ &=\sin ε\sin λ\cos β+\cos ε\sin β\\[2ex] \cos α\cos δ &=\cos λ\cos β\\[2ex] \sin α\cos δ &=\cos ε\sin λ\cos β-\sin ε\sin β \end{align}
// Equatorial coordinates are referenced to the Earth's rotational axis.
// 赤道坐标结构
type Equatorial struct {
RA unit.RA // Right ascension (α)赤经(时角)
Dec unit.Angle // Declination (δ)赤纬
}
// EclToEq converts ecliptic coordinates to equatorial coordinates.
// 黄道转赤道
func (eq *Equatorial) EclToEq(ecl *Ecliptic, ε *Obliquity) *Equatorial {
eq.RA, eq.Dec = EclToEq(ecl.Lon, ecl.Lat, ε.S, ε.C)
return eq
}
// EclToEq converts ecliptic coordinates to equatorial coordinates.
//
// λ: ecliptic longitude coordinate to transform
// β: ecliptic latitude coordinate to transform
// sε: sine of obliquity of the ecliptic
// cε: cosine of obliquity of the ecliptic
//
// Results:
// α: right ascension赤经(时角)
// δ: declination赤纬
// 黄道转赤道
func EclToEq(λ, β unit.Angle, sε, cε float64) (α unit.RA, δ unit.Angle) {
sλ, cλ := λ.Sincos()
sβ, cβ := β.Sincos()
α = unit.RAFromRad(math.Atan2(sλ*cε-(sβ/cβ)*sε, cλ)) // (13.3) p. 93
δ = unit.Angle(math.Asin(sβ*cε + cβ*sε*sλ)) // (13.4) p. 93
return
}
5.3 地平转赤道($φ,A,h\ \Rightarrow\ α,δ$)
\begin{align} \sin δ &=\sin φ\sin h-\cos φ\cos h\cos A\\[2ex] \cos δ\cos α &=-\cos φ\sin h-\sin φ\cos h\cos A\\[2ex] \cos δ\sin α &=-\sin A\cos h \end{align}
// HzToEq transforms horizontal coordinates to equatorial coordinates.
//
// Sidereal time st must be consistent with the equatorial coordinates
// in the sense that if coordinates are apparent, sidereal time must be
// apparent as well.
// 地平转赤道
func (eq *Equatorial) HzToEq(hz *Horizontal, g globe.Coord, st unit.Time) *Equatorial {
eq.RA, eq.Dec = HzToEq(hz.Az, hz.Alt, g.Lat, g.Lon, st)
return eq
}
// HzToEq transforms horizontal coordinates to equatorial coordinates.
//
// A: azimuth方位角
// h: elevation仰角
// φ: latitude of observer on Earth观测纬度
// ψ: longitude of observer on Earth观测经度
// st: sidereal time at Greenwich at time of observation.恒星时
//
// Sidereal time must be consistent with the equatorial coordinates
// in the sense that tf coordinates are apparent, sidereal time must be
// apparent as well.
// 恒星时必须和所给条件保持一致
//
// Results:
//
// α: right ascension赤经(时角)
// δ: declination赤纬
// 地平转赤道
func HzToEq(A, h, φ, ψ unit.Angle, st unit.Time) (α unit.RA, δ unit.Angle) {
sA, cA := A.Sincos()
sh, ch := h.Sincos()
sφ, cφ := φ.Sincos()
H := math.Atan2(sA, cA*sφ+sh/ch*cφ)
α = unit.RAFromRad(st.Rad() - ψ.Rad() - H)
δ = unit.Angle(math.Asin(sφ*sh - cφ*ch*cA))
return
}
5.4 赤道转地平($φ,α,δ\ \Rightarrow\ A,h$)
\begin{align} \sin h &= \sin φ\sin δ+\cos φ\cos δ\cos α\\[2ex] \cos A\cos h &=-\cos φ\sin δ+\sin φ\cos δ\cos α\\[2ex] \sin A\cos h &=\cos δ\sin α \end{align}
// Horizontal coordinates are referenced to the local horizon of an observer
// on the surface of the Earth.
// 地平坐标结构
type Horizontal struct {
Az unit.Angle // Azimuth (A)方位角
Alt unit.Angle // Altitude (h)仰角
}
// EqToHz computes Horizontal coordinates from equatorial coordinates.
//
// Argument g is the location of the observer on the Earth. Argument st
// is the sidereal time at Greenwich.
//
// Sidereal time must be consistent with the equatorial coordinates.
// If coordinates are apparent, sidereal time must be apparent as well.
// 赤道转地平
func (hz *Horizontal) EqToHz(eq *Equatorial, g *globe.Coord, st unit.Time) *Horizontal {
hz.Az, hz.Alt = EqToHz(eq.RA, eq.Dec, g.Lat, g.Lon, st)
return hz
}
// EqToHz computes Horizontal coordinates from equatorial coordinates.
//
// α: right ascension coordinate to transform
// δ: declination coordinate to transform
// φ: latitude of observer on Earth
// ψ: longitude of observer on Earth
// st: sidereal time at Greenwich at time of observation.
//
// Sidereal time must be consistent with the equatorial coordinates.
// If coordinates are apparent, sidereal time must be apparent as well.
//
// Results:
//
// A: azimuth of observed point, measured westward from the South.
// h: elevation, or height of observed point above horizon.
// 赤道转地平
func EqToHz(α unit.RA, δ, φ, ψ unit.Angle, st unit.Time) (A, h unit.Angle) {
H := st.Rad() - ψ.Rad() - α.Rad()
sH, cH := math.Sincos(H)
sφ, cφ := φ.Sincos()
sδ, cδ := δ.Sincos()
A = unit.Angle(math.Atan2(sH, cH*sφ-(sδ/cδ)*cφ)) // (13.5) p. 93
h = unit.Angle(math.Asin(sφ*sδ + cφ*cδ*cH)) // (13.6) p. 93
return
}
