第十一章 地球球体 The Earth’s Globe

1. 椭球体

　　天文学上，通常我们将地球看做一个近似的椭球体。如下图， 所以子午圈截面为一个椭圆。如下图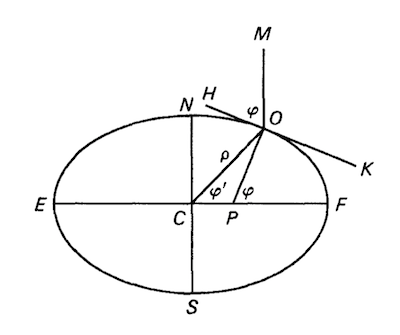， 　　假设上图中$C$为地心，$N$为北极，$S$为南极，$CF$为赤道半径，$NC = b, CF = a$,$O$为观察点，$HK$为地平面，$OP\perp HK$,$OM//SN$，$OM$与$OH$的夹角是$φ$，$CF$与$CO$的夹角是$φ’$，$CO$的长度为$\rho$
　　则$φ$为$O$点的地理纬度，$\angle OPF = φ$，$φ’$为$O$点的地心纬度,$\rho$为$O$点的地心半径,在极点和赤道上$φ=φ′$，在其它纬度上$|φ′|<|φ|$
　　地心纬度$φ’$与地理纬度$φ$的关系为：$\tan φ′=\frac {b^2}{a^2} \tan φ，$(推导)
　　由椭球体扁率$f=\frac {a-b}a$,可知$b=a(1-f)$,子午圈椭圆离心率 \begin{align} e &= \frac ca\\[2ex] & = \frac {\sqrt {a^2-b^2}}{a}\\[2ex] & = \sqrt {2f-f^2} \end{align} 　　地心纬度$φ’$对应的归化纬度$u$,有 \begin{cases} \tan φ’ = \frac ba \tan u\\[2ex] \tan u = \frac ba \tan φ\\[2ex] \end{cases} 且 \begin{cases} \rho \cos φ’ = a\cos u, \ (相当于子午圈椭圆上观察点O的x坐标)\\[2ex] \rho \sin φ’ = b\sin u, \ (相当于子午圈椭圆上观察点O的y坐标) \end{cases} 　　如果观察点的海拔高度为$H$,且$\rho$以赤道半径$a$为单位，则有 \begin{cases} \rho \cos φ’ = cos u + \frac Ha\cos φ\\[2ex] \rho \sin φ’ = \frac ba\sin u + \frac Ha\sin φ \end{cases}

// Ellipsoid represents an ellipsoid of revolution.
//
// Typical unit for Er is Km.
// 地球椭球体
type Ellipsoid struct {
	Er float64 // equatorial radius 赤道半径
	Fl float64 // flattening 地球扁率
}

// IAU 1976 values.  Radius in Km.
var Earth76 = Ellipsoid{Er: 6378.14, Fl: 1 / 298.257}

// A returns equatorial radius in units of e.Er.
//
// A is a common identifier for equatorial radius.
// 子午圈椭圆长半轴（赤道半径）
func (e Ellipsoid) A() float64 {
	return e.Er
}

// B returns polar radius in units of e.ER.
//
// B is a common identifier for polar radius.
//
// 子午圈椭圆短半轴（地心到极点的距离）
func (e Ellipsoid) B() float64 {
	return e.Er * (1 - e.Fl)
}

// Eccentricity of a meridian.
// 子午圈椭圆离心率
func (e Ellipsoid) Eccentricity() float64 {
	return math.Sqrt((2 - e.Fl) * e.Fl)
}

// ParallaxConstants computes parallax constants ρ sin φ′ and ρ cos φ′.
//
// Arguments are geographic latitude φ and height h above the ellipsoid.
// For e.Er in Km, h must be in meters.
// 海拔为h的观察点对应的ρ sin φ′，ρ cos φ′
func (e Ellipsoid) ParallaxConstants(φ unit.Angle, h float64) (s, c float64) {
	boa := 1 - e.Fl
	su, cu := math.Sincos(math.Atan(boa * φ.Tan()))
	s, c = φ.Sincos()
	hoa := h * 1e-3 / e.Er
	return su*boa + hoa*s, cu + hoa*c
}

2. 其他椭球公式

　　在椭球上给定的一点，地理纬度与地心纬度的差值为：$φ - φ′ = 692”.73sin(2φ) - 1”.16sin(4φ)$
　　当$u=45°$时，$φ-φ′$达到最大值。 如果$φ_0$和$φ_0′$是此时相应的地理纬度和地心纬度，我们有：$$tan(φ_0) = a/b，tan(φ_0′) = b/a， φ_0+φ_0′=90°$$ 对于IAU1976($a = 6378.14km,b = 6356.755km,f=\frac {1}{298.257}$) 有 \begin{align} φ_0 = 45°05′46”.36,\\[2ex] φ_0′ = 44°54′13”.64,\\[2ex] φ_0 - φ_0′ = 11′32”.73 \end{align} 　　海平面上，$$\rho =0.9983271+0.0016764\cos {2φ}-0.0000035\cos {4φ}$$ 　　同纬度$φ$的圆的半径：$$R_p = \frac {a\cos φ}{\sqrt{(1-e^2\sin^2φ)}}$$ 　　因此，在同一纬度$φ$上，经度变化1度，相应的长度变化为$(π/180)R_p$,线速度为$ωR_p$,其中$ω = 7.292114992*10^{-5}(弧度/秒)$
　　地球子午圈的曲率半径，在纬度$φ$：$$R_m=\frac {a(1-e^2)}{(1-e^2\sin ^2 φ)^{\frac 32}}$$ 且纬度变化1度，相应的长度变化：$(π/180)R_m$,在赤道时，$R_m$达到最小值，值为$a(1-e^2)=6335.44km$， 在极点时达到最大值，值为$\frac {a}{\sqrt {1-e^2}}=6399.60km$

// Rho is distance from Earth center to a point on the ellipsoid at latitude φ.
//
// Result unit is fraction of the equatorial radius.
// 海平面上，ρ值计算
func Rho(φ unit.Angle) float64 {
	// Magic numbers...
	return .9983271 + .0016764*φ.Mul(2).Cos() - .0000035*φ.Mul(4).Cos()
}

// RadiusAtLatitude returns the radius of the circle that is the parallel of
// latitude φ.
//
// Result unit is same as e.Er (typically Km.)
// 同纬度圆半径
func (e Ellipsoid) RadiusAtLatitude(φ unit.Angle) float64 {
	s, c := φ.Sincos()
	return e.A() * c / math.Sqrt(1-(2-e.Fl)*e.Fl*s*s)
}

// OneDegreeOfLongitude returns the length of one degree of longitude.
//
// Argument rp is the radius of a circle that is a parallel of latitude
// (as returned by Ellipsoid.RadiusAtLatitude.)
//
// Result is distance along one degree of the circle, in same units as rp.
// 同纬度，计算经度变化1度时长度变化的值
func OneDegreeOfLongitude(rp float64) float64 {
	return rp * math.Pi / 180
}

// RotationRate1996_5 is the rotational angular velocity of the Earth
// with respect to the stars at the epoch 1996.5.
//
// Unit is radian/second.
const RotationRate1996_5 = 7.292114992e-5

// RadiusOfCurvature of meridian at latitude φ.
//
// Result in units of e.ER, typically Km.
// 纬度为φ，子午圈曲率半径
func (e Ellipsoid) RadiusOfCurvature(φ unit.Angle) float64 {
	s := φ.Sin()
	e2 := (2 - e.Fl) * e.Fl
	return e.A() * (1 - e2) / math.Pow(1-e2*s*s, 1.5)
}

// OneDegreeOfLatitude returns the length of one degree of latitude.
//
// Argument rm is the radius of curvature along a meridian.
// (as returned by Ellipsoid.RadiusOfCurvature.)
// Result is distance in units of rm along one degree of the meridian.
// 同经度，计算纬度变化1度时长度变化的值
func OneDegreeOfLatitude(rm float64) float64 {
	return rm * math.Pi / 180
}

3. 地表两点间的距离

　　假设经纬度是分别是$(L_1,φ_1),(L_2,φ_2)$，且这两点在海平面。 　　如果精度要求不高，可以把地球看作球形，平均半径为6371km。使用下式可得到两点间的角距离：$$\cos d=\sin φ_1\sin φ_2 +\cos φ_1\cos φ_2\cos(L_1-L_2)$$ 那么$$s = \frac {6371πd}{180}$$ 　　高精度计算可使用以下方法： $$F=\frac {φ_1+φ_2}{2},G=\frac {φ_1-φ_2}{2},\lambda = \frac {L_1-L_2}{2}$$ $$S = \sin^2G\cos^2\lambda+\cos^2F\sin^2\lambda$$ $$C = \cos^2G\cos^2\lambda+\sin^2F\sin^2\lambda$$ $$\tan ω = \sqrt{\frac SC}$$ $$R=\frac{\sqrt{SC}}{ω}$$ $$D=2ωa,H_1=\frac{3R-1}{2C},H_2=\frac{3R+1}{2S}$$ $$s=D(1+fH_1\sin^2F\cos^2G-fH_2\cos^2F\sin^2G)$$

// Distance is distance between two points measured along the surface
// of an ellipsoid.
//
// Accuracy is much better than that of ApproxAngularDistance or
// ApproxLinearDistance.
//
// Result unit is units of e.Er, typically Km.
// 地表两点距离
func (e Ellipsoid) Distance(c1, c2 Coord) float64 {
	// From AA, ch 11, p 84.
	s2f, c2f := sincos2((c1.Lat + c2.Lat) / 2)
	s2g, c2g := sincos2((c1.Lat - c2.Lat) / 2)
	s2λ, c2λ := sincos2((c1.Lon - c2.Lon) / 2)
	s := s2g*c2λ + c2f*s2λ
	c := c2g*c2λ + s2f*s2λ
	ω := math.Atan(math.Sqrt(s / c))
	r := math.Sqrt(s*c) / ω
	d := 2 * ω * e.Er
	h1 := (3*r - 1) / (2 * c)
	h2 := (3*r + 1) / (2 * s)
	return d * (1 + e.Fl*(h1*s2f*c2g-h2*c2f*s2g))
}

func sincos2(x unit.Angle) (s2, c2 float64) {
	s, c := x.Sincos()
	return s * s, c * c
}