第五章 迭代 Iteration

1. 什么是迭代算法

　　迭代法（英语：Iterative Method），在计算数学中，迭代是通过从一个初始估计出发寻找一系列近似解来解决问题（一般是解方程或者方程组）的数学过程，为实现这一过程所使用的方法统称。

　　跟迭代法相对应的是直接法（或者称为一次解法），即一次性解决问题，例如通过开方解决方程 $ x^{2}=4$。一般如果可能，直接解法总是优先考虑的。但当遇到复杂问题时，特别是在未知量很多，方程为非线性时，我们无法找到直接解法（例如五次以及更高次的代数方程没有解析解，参见阿贝尔定理），这时候或许可以通过迭代法寻求方程（组）的近似解。

　　最常见的迭代法是牛顿法。其他还包括最速下降法、共轭迭代法、变尺度迭代法、最小二乘法、线性规划、非线性规划、单纯型法、惩罚函数法、斜率投影法、遗传算法、模拟退火等等。

　　以上是 wiki 上对迭代算法的描述，可以看出，迭代法的主要用途就是求解近似根，这一点我们再第三章插值函数逆推插值点的介绍中已经得到了运用。下面我们主要介绍牛顿迭代法和二分迭代法。

2. 牛顿迭代法

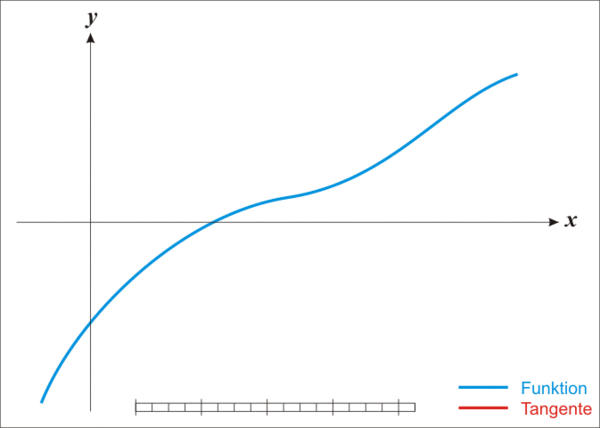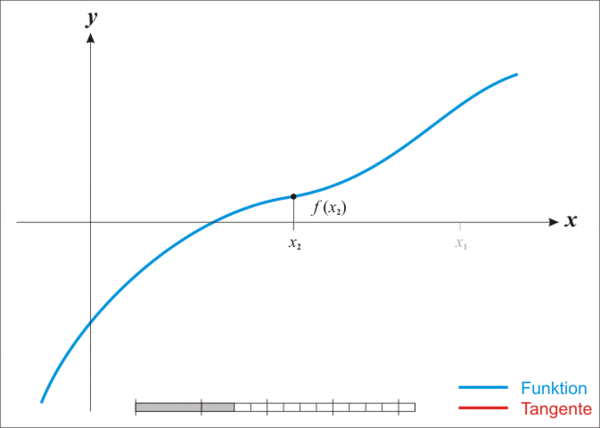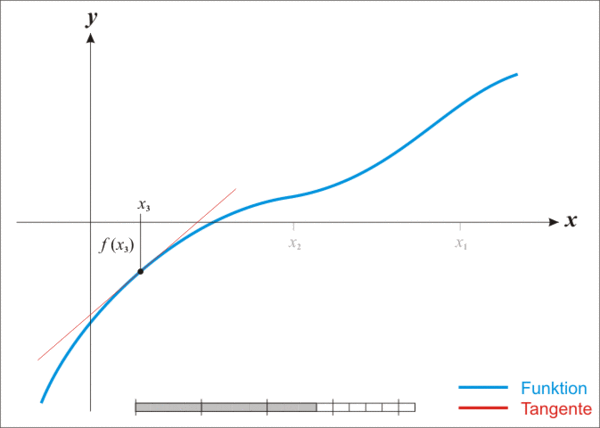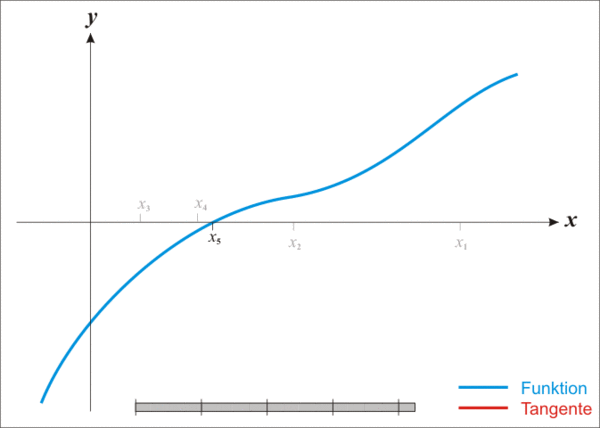
　　首先，选择一个接近函数$f(x)$零点的 $x_0$，计算相应的 $f(x_0)$和切线斜率 $f’(x_0)$。然后我们计算穿过点 $(x_0,f(x_0))$并且斜率为 $f’(x_0)$的直线和 $x$轴的交点的 $x$坐标，也就是求如下方程的解： $$0=(x-x_0)f’(x_0)+f(x_0)$$ 　　我们将新求得的点的$x$坐标命名为$x_1$，通常$x_1$会比$x_0$更接近方程$f(x)=0$的解。因此我们现在可以利用$x_1$开始下一轮迭代。迭代公式可化简为如下所示： $$x_{n+1}=x_n - \frac {f(x_n)}{f’(x_n)}$$ 　　已经证明，如果$f’$是连续的，并且待求的零点$x$是孤立的，那么在零点$x$周围存在一个区域，只要初始值$x_0$位于这个邻近区域内，那么牛顿法必定收敛。

　　并且，如果$f’(x)\neq 0$，那么牛顿法将具有平方收敛的性能。粗略的说，这意味着每迭代一次，牛顿法结果的有效数字将增加一倍。

// BetterFunc is a convience type definition.
type BetterFunc func(float64) float64

// DecimalPlaces iterates to a fixed number of decimal places.
//
// Inputs are an improvement function, a starting value, the number of
// decimal places desired in the result, and an iteration limit.
// better 为迭代公式，start 为起始点，places 为视作迭代结束的最大精度值的小数点位数,
// maxIterations 为迭代最大次数
func DecimalPlaces(better BetterFunc, start float64, places, maxIterations int) (float64, error) {
	d := math.Pow(10, float64(-places))
	for i := 0; i < maxIterations; i++ {
		n := better(start)
		if math.Abs(n-start) < d {
			return n, nil
		}
		start = n
	}
	return 0, errors.New("Maximum iterations reached")
}

// FullPrecison iterates to (nearly) the full precision of a float64.
//
// To allow for a little bit of floating point jitter, FullPrecision iterates
// to 15 significant figures, which is the maximum number of full significant
// figures representable in a float64, but still a couple of bits shy of the
// full representable precision.
// 和 DecimalPlaces 功能类似，只不过默认迭代结束的标志为小于float64的最大精度15
func FullPrecision(better BetterFunc, start float64, maxIterations int) (float64, error) {
	for i := 0; i < maxIterations; i++ {
		n := better(start)
		if math.Abs((n-start)/n) < 1e-15 {
			return n, nil
		}
		start = n
	}
	return 0, errors.New("Maximum iterations reached")
}

3. 二分迭代法

　　二分迭代法，顾名思义，就是计算中点的函数值，并与当前低值和高值比较，

• 若与低值同号，则把该值作为新的低值，继续迭代

• 若与高值同号，则把该值作为新的高值，继续迭代

// RootFunc is a convience type definition.
type RootFunc func(float64) float64

// BinaryRoot finds a root between given bounds by binary search.
//
// Inputs are a function on x and the bounds on x.  A root must exist between
// the given bounds, otherwise the result is not meaningful.
// 因为float64 的小数bit位最多为52位(10进制为15位有效数字)，
// 即每次迭代理论上能提升一位精度，所以最多52次就应该跳出迭代
func BinaryRoot(f RootFunc, lower, upper float64) float64 {
	yLower := f(lower)
	var mid float64
	for j := 0; j < 52; j++ {
		mid = (lower + upper) / 2
		yMid := f(mid)
		if yMid == 0 {
			break
		}
		if math.Signbit(yLower) == math.Signbit(yMid) { // 与低值同号，替代低值
			lower = mid
			yLower = yMid
		} else {
			upper = mid //与高值同号，替换高值
		}
	}
	return mid
}